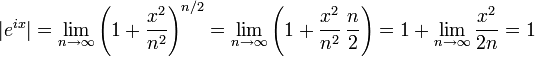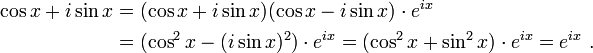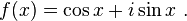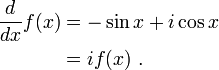In fact, susscees has its own function.
恆心是持之以恆的慢工
毅力是堅持到底的決心
勇氣是不被挫折打倒的動力
這三者缺一不可!!
台灣的流行音樂..........【台灣流行音樂】
台灣流行音樂有幾大特色:
一、KTV化—必須要簡單、反覆到人人都可以在KTV裡放聲高唱,方能大紅大紫
二、吉他化—許多創作人一開始接觸的樂器即為吉他,而吉他慣用的和絃進行便深深地宰制了國語流行歌曲的和聲架構(其實仍是等於換湯不換藥—旋律與歌詞更改,和絃進行類似)
三、簡單化—根據模仿的原理,國語歌曲在東施效顰時,勢必模仿部份後開始炒作,譬如R&B現象、哈韓哈日現象、擷取前段卻誠意不足地反覆刺激聽眾耳朵,甚至將原作之延伸發展捨去等現象
例A:平井堅之《Gaining Through Losing》V.S. F4《流星雨》—R&B的背景合音、複雜的絃樂編曲、中段R&B橋段全數捨去
例B、Al Jarreau《Morning》V.S. 張惠妹《一夜情》—只留開頭旋律與編曲風味,原曲後段轉調發展及即興全數捨去
台灣音樂創作人來源:
一、古典科班出身:黃韻玲、林隆璇…
二、民歌手︰李宗盛、游鴻明、張宇、陳綺貞…(註︰這裡所指民歌手,並非指參與民歌運動之早期創作者,而是泛指曾駐唱遊走於「民歌西餐廳」之自彈自唱者)
三、玩樂團︰庾澄慶、伍佰、五月天、張雨生、伍思凱、黃品源…
四、音樂製作助理︰陳昇…(許多從事幕後工作如編曲家、錄音師、樂手、經紀者亦為大宗)
前三項之來源還有可能由參加音樂大賽或唱片公司甄選而來,真正自我引薦或被星探發掘的情形,大多是發掘「藝人」的管道,而非發掘「創作人」的管道。
以下還有些國語流行歌曲的音樂分析,它們與原曲的動機、編曲、和絃、曲式,甚至連配器都很相似:
1. 黃舒駿《雁渡寒潭》 V.S. Elton John《Sixty Years On》
2. 周華健《寂寞的眼》 V.S. Dennis DeYoung《Call Me》
3. 黃品源《你怎麼捨得我難過》 V.S. Lionel Richie《Hello》
4. 庾澄慶《讓你媽媽New一下》 V.S. Earth Wind & Fire《Let's Groove》
5. 庾澄慶《整晚的音樂》 V.S. Gloria Eastfan《Rhythm Is Gonna Get You》
6. 張惠妹《一夜情》 V.S. Al Jarreau《Morning》
高明的即為仿效之作,不高明的就叫抄襲。
另一個有趣的例子是形象包裝問題,在塑造偶像時,連外表、選歌風格、舉止、化妝方面,都可能有雷同之處,但這並不一定是蓄意的,而是整體形象訴求所致
例:凡妮莎(Vanesia Carlton)《A Thousand Miles》 V.S. 王力宏《在每一秒裡都想見到你》
安裝新的skyeye 1.3.3 在 ubuntu 10.10 下
http://blog.csdn.net/matrix_designer/article/details/6403796
-----------------------------------------------------------------------
http://fenxiangdizhi.5d6d.com/thread-54-1-1.html
http://blogimg.chinaunix.net/blog/upfile2/100115000033.pdf
http://ftp.snapgear.org/pub/snapgear/tools/arm-linux/arm-linux-tools-20080623.
http://www.uclinux.org/pub/uClinux/dist/uClinux-dist-20101026.tar.bz2
http://downloads.sourceforge.net/project/skyeye/skyeye-testsuits/skyeye-testsuite-1.3.2/skyeye-testsuite-1.3.2_rc1.tar.gz?r=http%3A%2F%2Fen.sourceforge.jp%2Fprojects%2Fsfnet_skyeye%2Fdownloads%2Fskyeye-testsuits%2Fskyeye-testsuite-1.3.2%2Fskyeye-testsuite-1.3.2_rc1.tar.gz%2F&ts=1321612068&use_mirror=nchc
sudo apt-get install libncurses5-dev
sudo apt-get install genromfs编译make;
sudo apt-get install libx11-dev
错误:gui/x.cc:48: fatal error: X11/xpm.h: 没有那个文件或目录
sudo apt-get install libxpm-dev
http://mypaper.pchome.com.tw/index/search/keyword=%E9%9B%BB%E8%85%A6%E6%A4%85&sfield=4
| ||||
| ||||
| ||||
http://hi.baidu.com/lovingjava/blog/item/85091aee5a2bdaf8cf1b3e7a.html
《一步步写嵌入式操作系统》环境配置2011-05-14 20:26最近在看一本书,叫《一步步写嵌入式操作系统》,感觉写的不错,让我想起以前看过的《Orange's一个操作系统的实现》,这书比那本书简单,毕竟这是写嵌入式的操作系统嘛,但是这本书的售后就不如那本书了,官方网站比《O》可要冷清多了,这就导致开发环境很难配置好,尤其是对于Linux外行来说就更难了。经过一天的琢磨,我总算把环境问题都给解决了,所以要赶紧记录下来以免以后忘了,顺便给其他学习《一步步写嵌入式操作系统》一书的人提供一点帮助。
1.首先从cygwin官网下载setup.exe,然后按照书中的提示安装就行了。(切记安装时选择gcc4和make组件)。建议安装的目录中不要有空格,我的安装目录是H:\cygwin\。(你们可以根据自己的情况选择其他的目录)
2.把从www.leeos.org上下载下来的leeos_tools_for_cygwin.tar.gz复制到H:\cygwin\usr中
3.打开cygwin,输入命令cd /usr
4.输入命令tar zxvf leeos_tools_for_Cygwin.tar.gz将刚才复制过来的压缩包解压到当前目录
5.输入命令echo "PATH=\$PATH:/usr/leeos_tools_for_Cygwin/bin">>/etc/profile,输入这个命令其实就是设置cygwin的环境变量,不信看一下H:\cygwin\etc中的profile文件,在最下面多了一句话PATH=$PATH:/usr/leeos_tools_for_Cygwin/bin。重启cygwin
6.按照书上说此时就可以用命令arm-elf-gcc来编译C文件了,但是我无论怎么试,总是说permission denied,原来是我们没有权限来运行arm-elf-gcc命令。
我们在H:\ARMOS\usr\leeos_tools_for_cygwin\bin目录下找到了arm-elf-gcc.exe,于是我们在命令行中输入chmod 777 /usr/leeos_tools_for_Cygwin/bin/arm-elf-gcc.exe,此命令就是设置arm-elf-gcc.exe的权限,让我们有权限来运行它。
7.这是再次试着用arm-elf-gcc来编译c文件,会发现有一个错误error trying to exec 'cc1': execvp: No such file or directory,这意味着cygwin找不到cc1命令,
我们搜索一下,发现在H:\ARMOS\usr\leeos_tools_for_cygwin\libexec\gcc\arm-elf\4.4.2目录下有我们想要的cc1.exe,
我们可以用之前用过的方法再设置一下cygwin的环境变量让cygwin能够找到该目录下的cc1.exe,
所以我们输入命令echo "PATH=\$PATH:/usr/leeos_tools_for_Cygwin/libexec/gcc/arm-elf/4.4.2">>/etc/profile,
此时再看一下H:\cygwin\etc中的profile文件,在最下面又多了一句话PATH=$PATH:/usr/leeos_tools_for_Cygwin/libexec/gcc/arm-elf/4.4.2,现在cygwin就能找到cc1.exe了。再次重启cygwin
8.现在在试一下用arm-elf-gcc来编译c文件,又会出现错误permission denied,这回我们一下就明白原因了,就是我们现在同样没有权限来运行cc1.exe,所以还用刚才的方法设置一下权限,这回输入chmod 777 /usr/leeos_tools_for_Cygwin/libexec/gcc/arm-elf/4.4.2/cc1.exe
9.如果在试着运行arm-elf-gcc来编译c文件的话,同样还会出现类似的permission denied和权限错误,所以我们干脆一下把需要设置的环境变量和权限都设置完。
所以,总结一下步骤
1.下载安装cygwin
2.将下载下来的leeos_tools_for_cygwin.tar.gz放到H:\cygwin\usr中,并用命令cd /usr和tar zxvf leeos_tools_for_Cygwin.tar.gz解压
3.设置环境变量,依次输入以下三条命令
echo "PATH=\$PATH:/usr/leeos_tools_for_Cygwin/bin">>/etc/profile
echo "PATH=\$PATH:/usr/leeos_tools_for_Cygwin/libexec/gcc/arm-elf/4.4.2">>/etc/profile
echo "PATH=\$PATH:/usr/leeos_tools_for_Cygwin/arm-elf/bin">>/etc/profile
然后重启cygwin
4.用chmod 777命令把刚才设置的三个目录下的所有exe文件都设置一下权限。(肯定有类似批处理的那种命令可以一下把所有exe文件都设置完,但是我对linux环境不怎么熟悉,所以在这里还是用的最原始的办法一个一个改,还好一共也没几个exe文件)
5.把skyeye.exe复制到H:\cygwin\usr\leeos_tools_for_Cygwin\bin中。这样就算把环境配置完了。呵呵,鼓捣了我一天啊,希望对有同样问题的人有帮助。
belovedtttl 2011-08-12 22:38 | 回复你好,留个qq 659346010 希望可以加我 相互讨论下
4
Kongcsdn 2011-09-18 13:46 | 回复你好,能不能把那个/etc/profile这个文件给我发一下啊
我的总是提示unexpected end of file.
5
gccman 2011-09-21 10:47 | 回复顶呱呱,不错,我也碰到同样问题,看了你这文章搞好了。以后的经验教训是碰到这类问题要认真执行下find命令。
6
lovingjava 2011-10-11 22:17 | 回复回复Kongcsdn:不好意思,一直没有登录百度空间,你现在还需要那个文件吗,如果需要,把邮箱给我,我给你发过去。
7
Kongcsdn 2011-10-12 20:53 | 回复回复lovingjava:啊,不用了。谢谢!嘿嘿,我自己又重装了一遍,现在好了!还是很感谢lz的热情~
9
farce 2011-10-27 09:06 | 回复 chmod 777 -R *
(其中的-R是递归处理,*代表所有文件)
sine和指數函式的關係式:
![]()
![]()
![]()
![]()
![]()

![]()
![]()

Furthermore, this allows for the definition of the trigonometric functions for complex arguments z:

Euler's formula
From Wikipedia, the free encyclopediaJump to: navigation, search- This article is about Euler's formula in complex analysis. For Euler's formula in algebraic topology and polyhedral combinatorics see Euler characteristic.
Euler's formula, named after Leonhard Euler, is a mathematical formula in complex analysis that establishes the deep relationship between the trigonometric functions and the complex exponential function. Euler's formula states that, for any real number x,Part of a series of articles on
The mathematical constant e
Natural logarithm ·Exponential function Applications in: compound interest ·Euler's identity & Euler's formula ·half-lives & exponential growth/decay Defining e: proof that e is irrational ·representations of e ·Lindemann–Weierstrass theorem People John Napier ·Leonhard Euler Schanuel's conjecture
Richard Feynman called Euler's formula "our jewel" and "one of the most remarkable, almost astounding, formulas in all of mathematics."[2]
Contents
[hide][edit] History
It was Johann Bernoulli who noted that [3]
Meanwhile, Roger Cotes, in 1714, discovered that
It was Euler (presumably around 1740) who turned his attention to the exponential function instead of logarithms, and obtained the correct formula now named after him. It was published in 1748, and his proof was based on the infinite series of both sides being equal. Neither of these men saw the geometrical interpretation of the formula: the view of complex numbers as points in the complex plane arose only some 50 years later (see Caspar Wessel).
[edit] Applications in complex number theory
This formula can be interpreted as saying that the function eix traces out the unit circle in the complex number plane as x ranges through the real numbers. Here, x is the angle that a line connecting the origin with a point on the unit circle makes with the positive real axis, measured counter clockwise and in radians. Three-dimensional visualization of Euler's formula. See also circular polarization.
Three-dimensional visualization of Euler's formula. See also circular polarization.
The original proof is based on the Taylor series expansions of the exponential function ez (where z is a complex number) and of sin x and cos x for real numbers x (see below). In fact, the same proof shows that Euler's formula is even valid for all complex numbers z.
A point in the complex plane can be represented by a complex number written in cartesian coordinates. Euler's formula provides a means of conversion between cartesian coordinates and polar coordinates. The polar form simplifies the mathematics when used in multiplication or powers of complex numbers. Any complex number z = x + iy can be written as
 is the argument of z—i.e., the angle between the x axis and the vector z measured counterclockwise and in radians—which is defined up to addition of 2π. Many texts write tan-1(y/x) instead of atan2(y,x) but this needs adjustment when x ≤ 0.
is the argument of z—i.e., the angle between the x axis and the vector z measured counterclockwise and in radians—which is defined up to addition of 2π. Many texts write tan-1(y/x) instead of atan2(y,x) but this needs adjustment when x ≤ 0.
Now, taking this derived formula, we can use Euler's formula to define the logarithm of a complex number. To do this, we also use the definition of the logarithm (as the inverse operator of exponentiation) that
Therefore, one can write:
Finally, the other exponential law
[edit] Relationship to trigonometry
Euler's formula provides a powerful connection between analysis and trigonometry, and provides an interpretation of the sine and cosine functions as weighted sums of the exponential function:
These formulas can even serve as the definition of the trigonometric functions for complex arguments x. For example, letting x = iy, we have:
[edit] Other applications
In differential equations, the function eix is often used to simplify derivations, even if the final answer is a real function involving sine and cosine. The reason for this is that the complex exponential is the eigenfunction of differentiation. Euler's identity is an easy consequence of Euler's formula.
In electrical engineering and other fields, signals that vary periodically over time are often described as a combination of sine and cosine functions (see Fourier analysis), and these are more conveniently expressed as the real part of exponential functions with imaginary exponents, using Euler's formula. Also, phasor analysis of circuits can include Euler's formula to represent the impedance of a capacitor or an inductor.
[edit] Definitions of complex exponentiation
Main articles: Exponentiation and Exponential functionThe exponential function ex for real values of x may be defined in a few different equivalent ways (see Characterizations of the exponential function). Several of these methods may be directly extended to give definitions of ez for complex values of z simply by substituting z in place of x and using the complex algebraic operations. In particular we may use either of the two following definitions which are equivalent. From a more advanced perspective, each of these definitions may be interpreted as giving the unique analytic continuation of ex to the complex plane.
[edit] Power series definition
For complex z
[edit] Limit definition
For complex z
[edit] Proofs
Various proofs of the formula are possible.
[edit] Using power series
Here is a proof of Euler's formula using power series expansions as well as basic facts about the powers of i:[5]
[edit] Using the limit definition
 The black point represents a complex number in the complex plane. Its absolute value is r, the distance from the origin. Its argument is φ, its angle in radians counterclockwise from the positive real axis.Here is a proof of Euler's formula starting with the definition
The black point represents a complex number in the complex plane. Its absolute value is r, the distance from the origin. Its argument is φ, its angle in radians counterclockwise from the positive real axis.Here is a proof of Euler's formula starting with the definition The exponential function ez can be defined as the limit of (1 + z/N)N, as N approaches infinity, and thus eiπ is the limit of (1 +iπ/N)N. In this animation N takes various increasing values from 1 to 100. The computation of (1 + iπ/N)N is displayed as the combined effect of N repeated multiplications in the complex plane, with the final point being the actual value of (1 +iπ/N)N. It can be seen that as N gets larger (1 +iπ/N)N approaches a limit of −1.
The exponential function ez can be defined as the limit of (1 + z/N)N, as N approaches infinity, and thus eiπ is the limit of (1 +iπ/N)N. In this animation N takes various increasing values from 1 to 100. The computation of (1 + iπ/N)N is displayed as the combined effect of N repeated multiplications in the complex plane, with the final point being the actual value of (1 +iπ/N)N. It can be seen that as N gets larger (1 +iπ/N)N approaches a limit of −1.
 and an argument defined by arg z = atan2(x,y) (atan2 is a variant of the arctangent function). In these terms, a complex multiplication z = z1z2 is performed by adding the arguments (arg(z) = arg(z1) + arg(z2)) and multiplying the absolute values (
and an argument defined by arg z = atan2(x,y) (atan2 is a variant of the arctangent function). In these terms, a complex multiplication z = z1z2 is performed by adding the arguments (arg(z) = arg(z1) + arg(z2)) and multiplying the absolute values ( ). (These facts are sometimes proved using Euler's theorem itself, but can alternatively be proved directly with algebra and trigonometry.) This is the basis for a two-step proof of Euler's theorem, which first calculates the absolute value of eix, and second calculates the argument of eix.
). (These facts are sometimes proved using Euler's theorem itself, but can alternatively be proved directly with algebra and trigonometry.) This is the basis for a two-step proof of Euler's theorem, which first calculates the absolute value of eix, and second calculates the argument of eix.
The first step is to calculate the absolute value of eix:
 . Therefore,
. Therefore,
 when θ is small and measured in radians. It can be derived using either geometry or calculus.) Therefore,
when θ is small and measured in radians. It can be derived using either geometry or calculus.) Therefore,
[edit] Using calculus
A well-known property of the real exponential function ex is that it equals its own derivative:
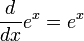 (where x is a real number).
(where x is a real number).
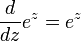 (where z is a complex number).
(where z is a complex number).
[edit] Using differential equations
Here is another proof using calculus. The starting assumption is the same as in the previous proof:

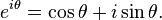

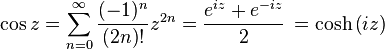

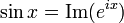
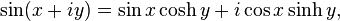
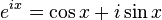

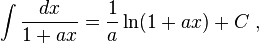


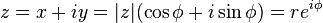

 the real part
the real part the imaginary part
the imaginary part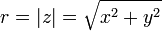 the
the 







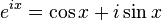
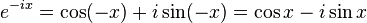


![\begin{align}
\cos x\cdot \cos y & = \frac{(e^{ix}+e^{-ix})}{2} \cdot \frac{(e^{iy}+e^{-iy})}{2} \\
& = \frac{1}{2}\cdot \frac{e^{i(x+y)}+e^{i(x-y)}+e^{i(-x+y)}+e^{i(-x-y)}}{2} \\
& = \frac{1}{2} \left[ \underbrace{ \frac{e^{i(x+y)} + e^{-i(x+y)}}{2} }_{\cos(x+y)} + \underbrace{ \frac{e^{i(x-y)} + e^{-i(x-y)}}{2} }_{\cos(x-y)} \right] \ .
\end{align}](http://upload.wikimedia.org/wikipedia/en/math/0/e/7/0e776e3123b92207c493f1485cf8471f.png)
![\begin{align}
\cos(nx) & = \mathrm{Re} \{\ e^{inx}\ \}
= \mathrm{Re} \{\ e^{i(n-1)x}\cdot e^{ix}\ \} \\
& = \mathrm{Re} \{\ e^{i(n-1)x}\cdot (e^{ix} + e^{-ix} - e^{-ix})\ \} \\
& = \mathrm{Re} \{\ e^{i(n-1)x}\cdot \underbrace{(e^{ix} + e^{-ix})}_{2\cos(x)} - e^{i(n-2)x}\ \} \\
& = \cos[(n-1)x]\cdot 2 \cos(x) - \cos[(n-2)x] \ .
\end{align}](http://upload.wikimedia.org/wikipedia/en/math/3/5/5/355d0c203746703fa4d33379a343b5db.png)
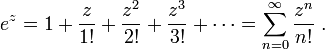
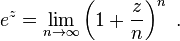

![\begin{align}
e^{ix} &{}= 1 + ix + \frac{(ix)^2}{2!} + \frac{(ix)^3}{3!} + \frac{(ix)^4}{4!} + \frac{(ix)^5}{5!} + \frac{(ix)^6}{6!} + \frac{(ix)^7}{7!} + \frac{(ix)^8}{8!} + \cdots \\[8pt]
&{}= 1 + ix - \frac{x^2}{2!} - \frac{ix^3}{3!} + \frac{x^4}{4!} + \frac{ix^5}{5!} - \frac{x^6}{6!} - \frac{ix^7}{7!} + \frac{x^8}{8!} + \cdots \\[8pt]
&{}= \left( 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \frac{x^6}{6!} + \frac{x^8}{8!} - \cdots \right) + i\left( x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \cdots \right) \\[8pt]
&{}= \cos x + i\sin x \ .
\end{align}](http://upload.wikimedia.org/wikipedia/en/math/8/7/9/8799ab90dd91d47cf82ea7b449556230.png)