sine和指數函式的關係式:
Relationship to exponential function and complex numbers
![]()
![]()
![]()
![]()
![]()

![]()
![]()

Furthermore, this allows for the definition of the trigonometric functions for complex arguments z:

Euler's formula
From Wikipedia, the free encyclopedia- This article is about Euler's formula in complex analysis. For Euler's formula in algebraic topology and polyhedral combinatorics see Euler characteristic.
Euler's formula, named after Leonhard Euler, is a mathematical formula in complex analysis that establishes the deep relationship between the trigonometric functions and the complex exponential function. Euler's formula states that, for any real number x,Part of a series of articles on
The mathematical constant e
Natural logarithm ·Exponential function Applications in: compound interest ·Euler's identity & Euler's formula ·half-lives & exponential growth/decay Defining e: proof that e is irrational ·representations of e ·Lindemann–Weierstrass theorem People John Napier ·Leonhard Euler Schanuel's conjecture
Richard Feynman called Euler's formula "our jewel" and "one of the most remarkable, almost astounding, formulas in all of mathematics."[2]
Contents
[hide][edit] History
It was Johann Bernoulli who noted that [3]
Meanwhile, Roger Cotes, in 1714, discovered that
It was Euler (presumably around 1740) who turned his attention to the exponential function instead of logarithms, and obtained the correct formula now named after him. It was published in 1748, and his proof was based on the infinite series of both sides being equal. Neither of these men saw the geometrical interpretation of the formula: the view of complex numbers as points in the complex plane arose only some 50 years later (see Caspar Wessel).
[edit] Applications in complex number theory
This formula can be interpreted as saying that the function eix traces out the unit circle in the complex number plane as x ranges through the real numbers. Here, x is the angle that a line connecting the origin with a point on the unit circle makes with the positive real axis, measured counter clockwise and in radians. Three-dimensional visualization of Euler's formula. See also circular polarization.
Three-dimensional visualization of Euler's formula. See also circular polarization.
The original proof is based on the Taylor series expansions of the exponential function ez (where z is a complex number) and of sin x and cos x for real numbers x (see below). In fact, the same proof shows that Euler's formula is even valid for all complex numbers z.
A point in the complex plane can be represented by a complex number written in cartesian coordinates. Euler's formula provides a means of conversion between cartesian coordinates and polar coordinates. The polar form simplifies the mathematics when used in multiplication or powers of complex numbers. Any complex number z = x + iy can be written as
 is the argument of z—i.e., the angle between the x axis and the vector z measured counterclockwise and in radians—which is defined up to addition of 2π. Many texts write tan-1(y/x) instead of atan2(y,x) but this needs adjustment when x ≤ 0.
is the argument of z—i.e., the angle between the x axis and the vector z measured counterclockwise and in radians—which is defined up to addition of 2π. Many texts write tan-1(y/x) instead of atan2(y,x) but this needs adjustment when x ≤ 0.
Now, taking this derived formula, we can use Euler's formula to define the logarithm of a complex number. To do this, we also use the definition of the logarithm (as the inverse operator of exponentiation) that
Therefore, one can write:
Finally, the other exponential law
[edit] Relationship to trigonometry
Euler's formula provides a powerful connection between analysis and trigonometry, and provides an interpretation of the sine and cosine functions as weighted sums of the exponential function:
These formulas can even serve as the definition of the trigonometric functions for complex arguments x. For example, letting x = iy, we have:
[edit] Other applications
In differential equations, the function eix is often used to simplify derivations, even if the final answer is a real function involving sine and cosine. The reason for this is that the complex exponential is the eigenfunction of differentiation. Euler's identity is an easy consequence of Euler's formula.
In electrical engineering and other fields, signals that vary periodically over time are often described as a combination of sine and cosine functions (see Fourier analysis), and these are more conveniently expressed as the real part of exponential functions with imaginary exponents, using Euler's formula. Also, phasor analysis of circuits can include Euler's formula to represent the impedance of a capacitor or an inductor.
[edit] Definitions of complex exponentiation
Main articles: Exponentiation and Exponential functionThe exponential function ex for real values of x may be defined in a few different equivalent ways (see Characterizations of the exponential function). Several of these methods may be directly extended to give definitions of ez for complex values of z simply by substituting z in place of x and using the complex algebraic operations. In particular we may use either of the two following definitions which are equivalent. From a more advanced perspective, each of these definitions may be interpreted as giving the unique analytic continuation of ex to the complex plane.
[edit] Power series definition
For complex z
[edit] Limit definition
For complex z
[edit] Proofs
Various proofs of the formula are possible.
[edit] Using power series
Here is a proof of Euler's formula using power series expansions as well as basic facts about the powers of i:[5]
[edit] Using the limit definition
 The black point represents a complex number in the complex plane. Its absolute value is r, the distance from the origin. Its argument is φ, its angle in radians counterclockwise from the positive real axis.Here is a proof of Euler's formula starting with the definition
The black point represents a complex number in the complex plane. Its absolute value is r, the distance from the origin. Its argument is φ, its angle in radians counterclockwise from the positive real axis.Here is a proof of Euler's formula starting with the definition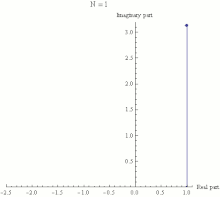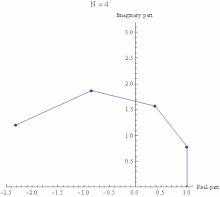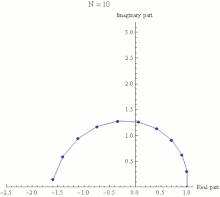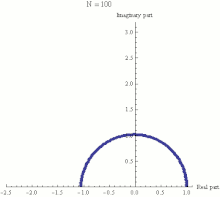 The exponential function ez can be defined as the limit of (1 + z/N)N, as N approaches infinity, and thus eiπ is the limit of (1 +iπ/N)N. In this animation N takes various increasing values from 1 to 100. The computation of (1 + iπ/N)N is displayed as the combined effect of N repeated multiplications in the complex plane, with the final point being the actual value of (1 +iπ/N)N. It can be seen that as N gets larger (1 +iπ/N)N approaches a limit of −1.
The exponential function ez can be defined as the limit of (1 + z/N)N, as N approaches infinity, and thus eiπ is the limit of (1 +iπ/N)N. In this animation N takes various increasing values from 1 to 100. The computation of (1 + iπ/N)N is displayed as the combined effect of N repeated multiplications in the complex plane, with the final point being the actual value of (1 +iπ/N)N. It can be seen that as N gets larger (1 +iπ/N)N approaches a limit of −1.
 and an argument defined by arg z = atan2(x,y) (atan2 is a variant of the arctangent function). In these terms, a complex multiplication z = z1z2 is performed by adding the arguments (arg(z) = arg(z1) + arg(z2)) and multiplying the absolute values (
and an argument defined by arg z = atan2(x,y) (atan2 is a variant of the arctangent function). In these terms, a complex multiplication z = z1z2 is performed by adding the arguments (arg(z) = arg(z1) + arg(z2)) and multiplying the absolute values ( ). (These facts are sometimes proved using Euler's theorem itself, but can alternatively be proved directly with algebra and trigonometry.) This is the basis for a two-step proof of Euler's theorem, which first calculates the absolute value of eix, and second calculates the argument of eix.
). (These facts are sometimes proved using Euler's theorem itself, but can alternatively be proved directly with algebra and trigonometry.) This is the basis for a two-step proof of Euler's theorem, which first calculates the absolute value of eix, and second calculates the argument of eix.
The first step is to calculate the absolute value of eix:
 . Therefore,
. Therefore,
 when θ is small and measured in radians. It can be derived using either geometry or calculus.) Therefore,
when θ is small and measured in radians. It can be derived using either geometry or calculus.) Therefore,
[edit] Using calculus
A well-known property of the real exponential function ex is that it equals its own derivative:
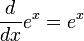 (where x is a real number).
(where x is a real number).
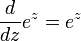 (where z is a complex number).
(where z is a complex number).
[edit] Using differential equations
Here is another proof using calculus. The starting assumption is the same as in the previous proof:

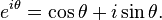

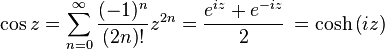

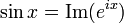
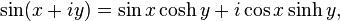
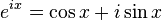



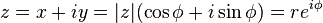

 the real part
the real part the imaginary part
the imaginary part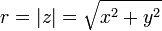 the
the 







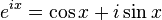
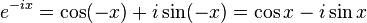


![\begin{align}
\cos x\cdot \cos y & = \frac{(e^{ix}+e^{-ix})}{2} \cdot \frac{(e^{iy}+e^{-iy})}{2} \\
& = \frac{1}{2}\cdot \frac{e^{i(x+y)}+e^{i(x-y)}+e^{i(-x+y)}+e^{i(-x-y)}}{2} \\
& = \frac{1}{2} \left[ \underbrace{ \frac{e^{i(x+y)} + e^{-i(x+y)}}{2} }_{\cos(x+y)} + \underbrace{ \frac{e^{i(x-y)} + e^{-i(x-y)}}{2} }_{\cos(x-y)} \right] \ .
\end{align}](http://upload.wikimedia.org/wikipedia/en/math/0/e/7/0e776e3123b92207c493f1485cf8471f.png)
![\begin{align}
\cos(nx) & = \mathrm{Re} \{\ e^{inx}\ \}
= \mathrm{Re} \{\ e^{i(n-1)x}\cdot e^{ix}\ \} \\
& = \mathrm{Re} \{\ e^{i(n-1)x}\cdot (e^{ix} + e^{-ix} - e^{-ix})\ \} \\
& = \mathrm{Re} \{\ e^{i(n-1)x}\cdot \underbrace{(e^{ix} + e^{-ix})}_{2\cos(x)} - e^{i(n-2)x}\ \} \\
& = \cos[(n-1)x]\cdot 2 \cos(x) - \cos[(n-2)x] \ .
\end{align}](http://upload.wikimedia.org/wikipedia/en/math/3/5/5/355d0c203746703fa4d33379a343b5db.png)
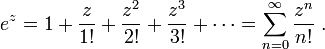
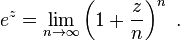

![\begin{align}
e^{ix} &{}= 1 + ix + \frac{(ix)^2}{2!} + \frac{(ix)^3}{3!} + \frac{(ix)^4}{4!} + \frac{(ix)^5}{5!} + \frac{(ix)^6}{6!} + \frac{(ix)^7}{7!} + \frac{(ix)^8}{8!} + \cdots \\[8pt]
&{}= 1 + ix - \frac{x^2}{2!} - \frac{ix^3}{3!} + \frac{x^4}{4!} + \frac{ix^5}{5!} - \frac{x^6}{6!} - \frac{ix^7}{7!} + \frac{x^8}{8!} + \cdots \\[8pt]
&{}= \left( 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \frac{x^6}{6!} + \frac{x^8}{8!} - \cdots \right) + i\left( x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \cdots \right) \\[8pt]
&{}= \cos x + i\sin x \ .
\end{align}](http://upload.wikimedia.org/wikipedia/en/math/8/7/9/8799ab90dd91d47cf82ea7b449556230.png)



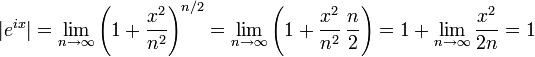







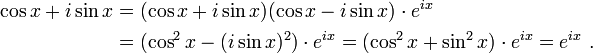
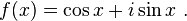
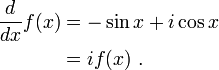
0 意見
張貼留言