δ函數
[上午10:08 | 0 意見 ]

 Dirac comb函數的傅立葉變換
Dirac comb函數的定義為

\Delta_T(t)\stackrel{\text{def}}{=}\sum_{n=-\infty}^{\infty}\delta(t-nT)
在電力工程中通常又稱作衝擊串（impulse train）或採樣函數 （sampling function）。其重要的傅立葉變換為：
\sum_{n=-\infty}^{\infty}\delta(t-nT)=\frac{1}{T}\sum_{k=-\infty}^{\infty}e^{i\frac{2\pi k}{T}t} \quad\stackrel{\mathcal{F}}{\longleftrightarrow}\quad \frac{1}{T}\sum_{k=-\infty}^{\infty}\delta\left(f-\frac{k}{T}\right)=\sum_{n=-\infty}^{\infty}e^{-i2\pi nTf}
這個變換在傅立葉變換家族中各個變換之間轉換上起關鍵作用。

傅立葉變換的卷積定理（convolution theorem）
這包括了傅立葉變換的時域卷積和頻域卷積：
\begin{align} x_1(t)\ast x_2(t) &\quad\stackrel{\mathcal{F}}{\longleftrightarrow}\quad X_1(f)\cdot X_2(f) \\ x_1(t)\cdot x_2(t) &\quad\stackrel{\mathcal{F}}{\longleftrightarrow}\quad X_1(f)\ast X_2(f) \end{align}
3. 泊松求和公式（Poisson summation formula）
由Dirac comb函數的傅立葉變換和卷積定理，容易證明泊松求和公式：
\begin{align} 1. \qquad &\sum_{n=-\infty}^{\infty}x(t-nT_0)=\frac{1}{T_0}\sum_{k=-\infty}^{\infty}X\left(\frac{k}{T_0}\right)e^{i\frac{2\pi k}{T_0}t} \\ 2. \qquad &\sum_{n=-\infty}^{\infty}x(nT)e^{-i2\pi nTf}=\frac{1}{T}\sum_{k=-\infty}^{\infty}X\left(f-\frac{k}{T}\right) \end{align}
若第1和第2公式中分別取 t = 0 和 f = 0 ，得到相同等式：
\sum_{n=-\infty}^{\infty}x(nT)=\frac{1}{T}\sum_{k=-\infty}^{\infty}X\left(\frac{k}{T}\right)
這表明，傅立葉變換時時域函數 x(t) 和頻域函數 X(f) 分別以 T 和 1 / T 為間隔採樣，則所有時域採樣點的總和與所有頻域採樣點擴大 1 / T 的總和相等。


狄拉克δ函數
Dirac delta is not strictly
http://en.wikipedia.org/wiki/Dirac_delta_function
http://zh.wikipedia.org/wiki/%E7%8B%84%E6%8B%89%E5%85%8B%CE%B4%E5%87%BD%E6%95%B0

Dirac delta is not strictly a function.
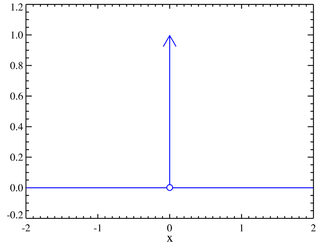
Plot of the Dirac delta function
and which is also constrained to satisfy the identity
  1. \delta(x) = 0 \mbox{ if } x \neq 0
  2. \int^{\infty}_{-\infty} \delta(x)\,dx = 1

這個才是δ函數最基本的定義，至於x=0時δ函數(x)=∞是合理的，就像英文維基中提到，他是希望他在x=0時到處都可能發生，因此在x=0時要把他定義成任何數字都可以。畢竟，這個函式並不能算是一個真正的函式。而且他最一開始的用意應該也不是為了解決訊號問題(從維基百科看看http://zh.wikipedia.org/w/index.php?title=%E4%BF%9D%E7%BD%97%C2%B7%E7%8B%84%E6%8B%89%E5%85%8B&variant=zh-hant發明這個符號的保羅．狄拉克應該是為了解決量子力學的問題的)
這個 δ函式有個好玩的地方，在於他想表達他的積分為1，而積分的最基本意義就是求與x軸的面積，代表著，這其實是一種極限，意味著x=0.001，而他y軸長度就等於1000，然後越來越逼近這個極限，讓我覺得，這就像長尾效應一樣，越小的數，乘以無限大，是很大的。代表著雖然你很小，小到是一條無法表示面積的線，他還是存在，他還是有面積的。因此給了他一個面積為1真的是很好玩。
我想，這個連結是給錯了，真正代表信號的是克羅內克爾δhttp://zh.wikipedia.org/w/index.php?title=%E5%85%8B%E7%BD%97%E5%86%85%E5%85%8B%E5%B0%94%CE%B4&variant=zh-tw
畢竟讓δ(x)=1(x=0),δ(x)=0(x≠0)這樣所有方程式去乘他才會是原來的方程式該點的位置(
x\left[ n\right] =\sum_{k}x\left[ k\right] \delta \left[ n-k\right])，也用了一個蠻特別式子去代表有一個一直往X軸上下方衝的含式，他跑了距離要為1這樣才會因為和原方程式相乘而到達該方程式的位置，畢竟，取樣定理(http://zh.wikipedia.org/wiki/%E9%87%87%E6%A0%B7%E5%AE%9A%E7%90%86)
的意義就在於好幾條線逼近該圓滑的方程式，就代表著該方程式，有一點像是積分是靠著好幾個極小的方塊加起來逼近就是該面積一樣。而他每條線的距離代表著每幾秒取一次的意思，因此當然是秒數越小越準，頻率越大越準。

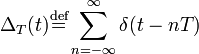
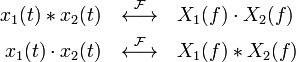
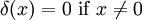
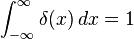
0 意見

張貼留言